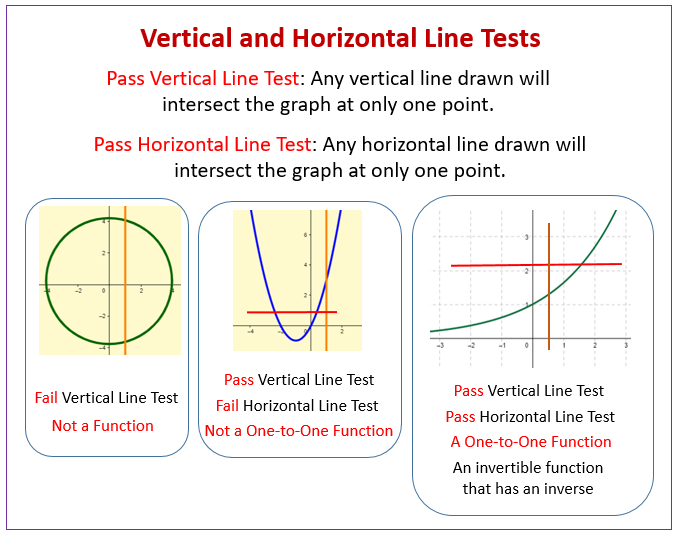
Aug 19, 19 · Also known as an injective function, a one to one function is a mathematical function that has only one y value for each x value, and only one x value for each y value Let's take y = 2x as an example Plugging in a number for x will result in a single output for y Also, plugging in a number for y will result in a single output for x BothTo prove relation reflexive, transitive, symmetric and equivalent;Use the horizontal line test to determine whether a function is onetoone;

Mathwords One To One Function
One to one function def
One to one function def-Definition of a onetoone function A function is a onetoone if no two different elements in D have the same element in R The definition of a one to one function can be written algebraically as follows Let x1 and x2 be any elements of DEmpty and Universal Relation;


1
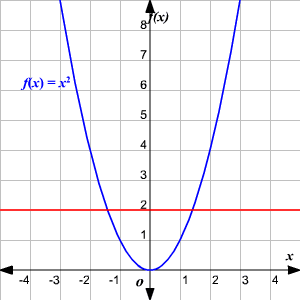
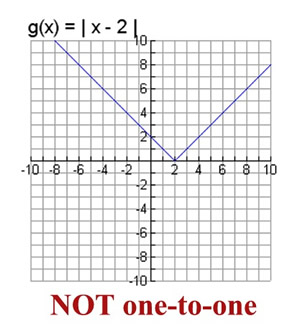
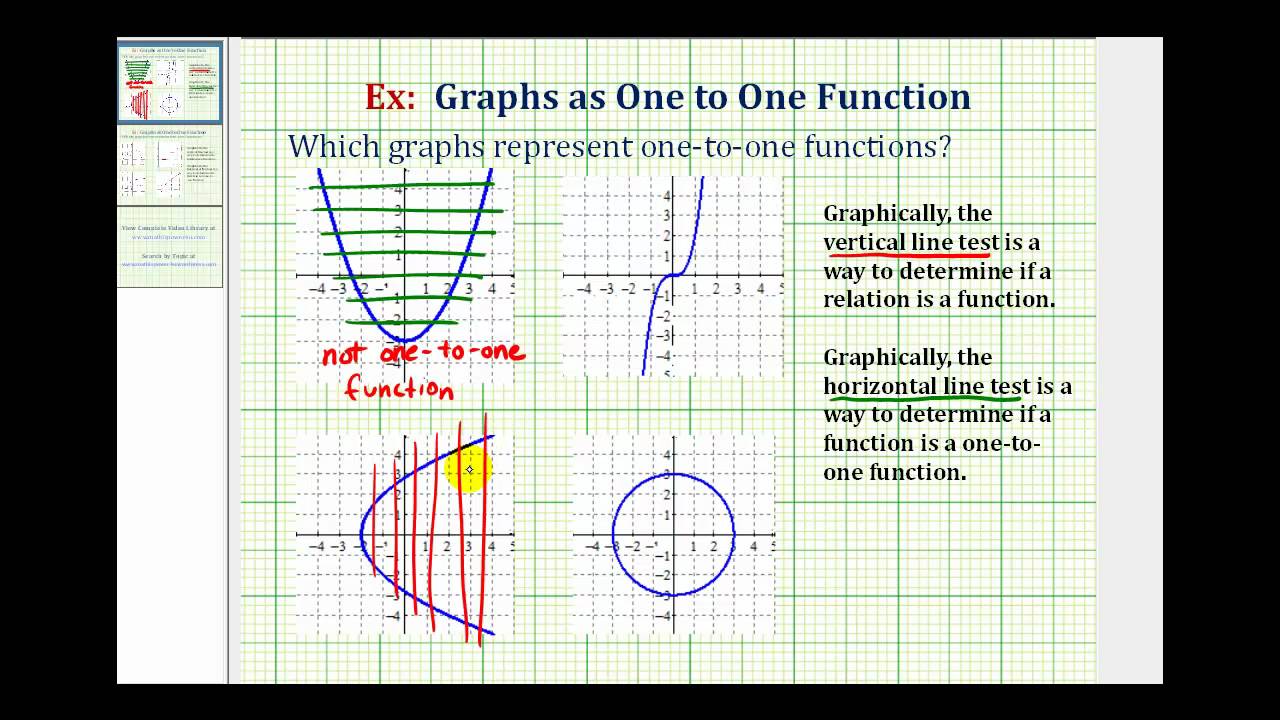
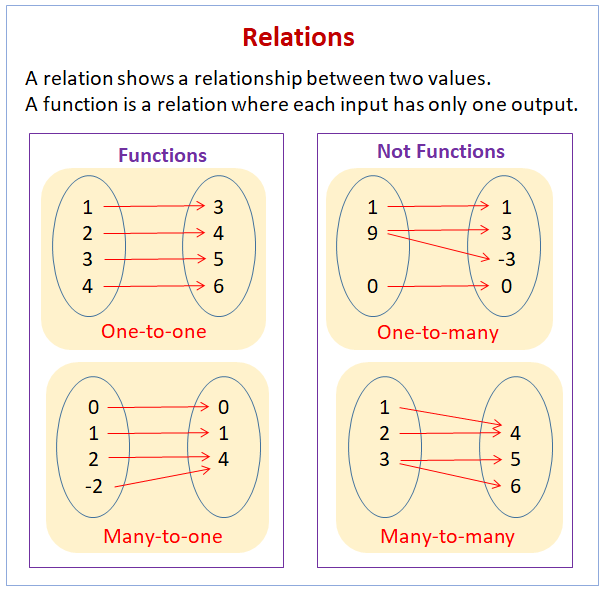
Then the function is not onetoone • If no horizontal line intersects the graph of the function more than once, then the function is onetoone What are OneToOne Functions?OnetoOne Function A function for which every element of the range of the function corresponds to exactly one element of the domain Onetoone is often written 11 Note y = f (x) is a function if it passes the vertical line testOnetoOne Function A function is a onetoone function if every element or yvalue in the range comes from a unique element or xvalue in the domain In other words, a function is a onetoone function if it never maps or associates two or more xvalues to the same yvalue Example Here is a more "advanced" definition
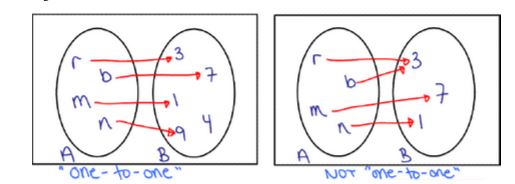
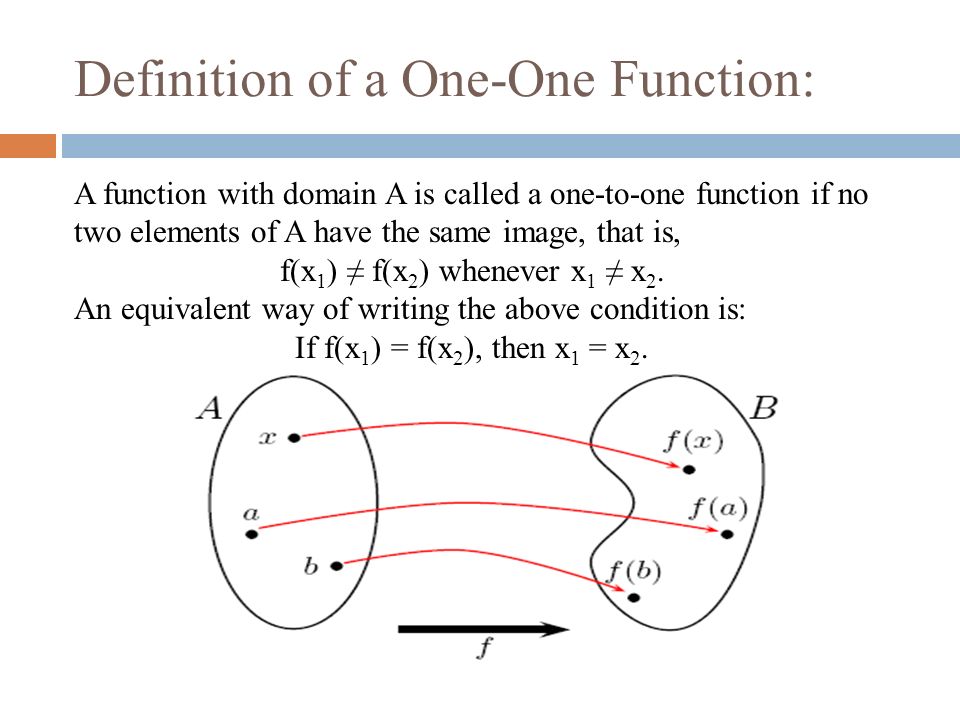
Oneonone definition is playing directly against a single opposing playerOnetoOne Functions A function f is 1 to 1 if no two elements in the domain of f correspond to the same element in the range of f In other words, each x in the domain has exactly one image in the range And, no y in the range is the image of more than one x in the domainTo prove oneone & onto (injective, surjective, bijective) Composite functions;
Covid19 has affected physical interactions between people Don't let it affect your learningDefine a onetoone function;Oct 14, 10 · Therefore, by definition a onetoone function is both into and onto But you say "an onto function from Y to X must exist" The "from Y to X" part might be what's tripping you up?


Functions Presentation Mathematics


Www Inf Unibz It Artale Dml Lectures Slides9 Functions Pdf
Theoretical definition A function f {0,1} * → {0,1} * is oneway if f can be computed by a polynomial time algorithm, but any polynomial time randomized algorithm that attempts to compute a pseudoinverse for f succeeds with negligible probability (The * superscript means any number of repetitions, see Kleene star)That is, for all randomized algorithms , all positive integers c and allDetermining if a set of points is a function and if a set of points is onetoone So behind me I have a set of points Function f is the set of points and I want to determine if this is a function So to determine whether it's function, for every x there's only one yAug 16, 19 · Definition OnetoOne (Injection) A function \({f}{A}\to{B}\) is said to be onetoone if \f(x_1) = f(x_2) \Rightarrow x_1=x_2\ for all elements \(x_1,x_2\in A\) A onetoone function is also called an injection, and we call a function injective if it is onetoone A function that is not onetoone is referred to as manytoone


Injective Function Wikipedia



5 1 Introduction To Functions
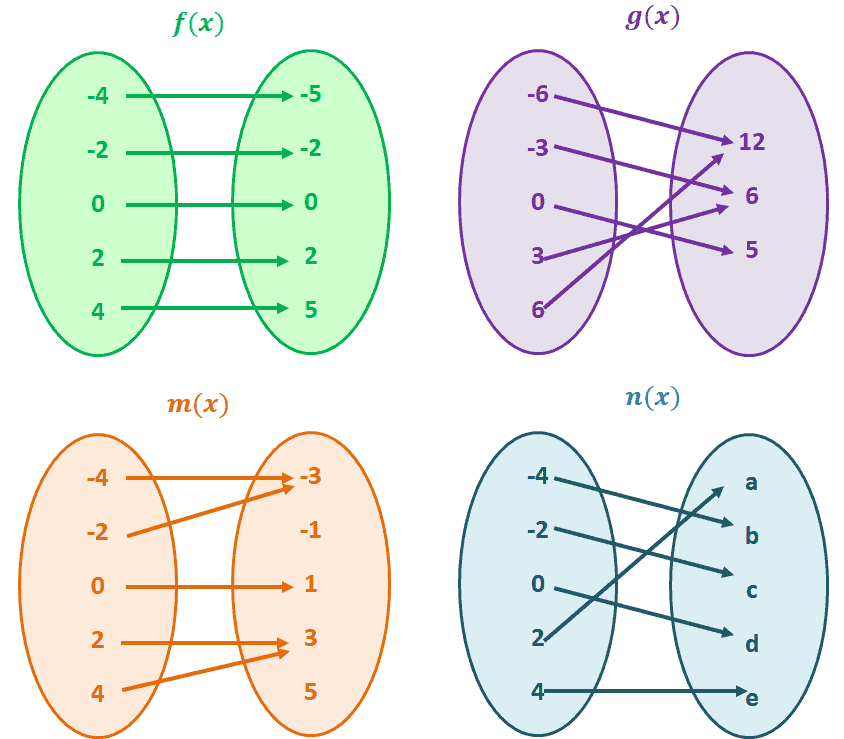
Give functions such as the one in Figure 6 a special name A function is onetoone if any two different inputs in the domain correspond to two different outputs in the rangeThat is, if and are two different inputs of a function then Put another way, a function is onetoone if no y in the range is the image of more than one x in the domainAlgebraic Test Definition 1 A function f is said to be onetoone (or injective) if f(x 1) = f(x 2) implies x 1 = x 2 Lemma 2 The function f is onetoone if andMar 10, 14 · We will prove by contradiction Let be a onetoone function as above but not onto Therefore, such that for every , Therefore, can be written as a onetoone function from (since nothing maps on to ) Similarly, we repeat this process to remove all elements from the codomain that are not mapped to by to obtain a new codomain is now a onetoone and onto function


One To One Functions


One To One Functions
May 29, 18 · f X → Y Function f is oneone if every element has a unique image, ie when f(x 1 ) = f(x 2 ) ⇒ x 1 = x 2 Otherwise the function is manyone How to check if function is oneone Method 1 In this method, we check for each and every element manually if it has unique imageInverse of function Proof questionsThe best way of proving a function to be one to one or onto is by using the definitions A function mathfA \rightarrow B/math is said to be one to one (injective) if for every mathx,y\in{A},/math mathf(x)=f(y)/math then mathx=y/ma



Strong One Way Function Cryptography Stack Exchange


Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture01 Handout Pdf
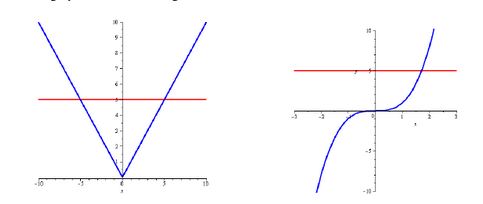
To prove that a function is $11$, we can't just look at the graph, because a graph is a small snapshot of a function, and we generally need to verify $11$ness on the whole domain of a function So though the Horizontal Line Test is a nice heuristic argument, it's not in itself a proofA function is a relation Therefore one can also talk about composition of functions Definition (composite function) Let g be a function from a set A to a set B, and let f be a function from B to a set C Then the composition of functions f and g, denoted by fg,So the given function is oneto one function 11th grade math From one to one function to Home Covid19 has led the world to go through a phenomenal transition Elearning is the future today Stay Home , Stay Safe and keep learning!!!


Function A Maths Dictionary For Kids Quick Reference By Jenny Eather


Injective Function Wikipedia
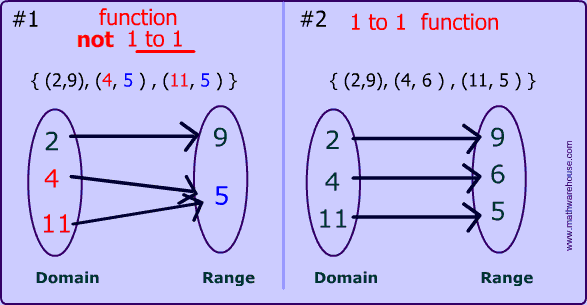
Remember that in a function, the input value must have one and only one value for the output There is a name for the set of input values and another name for the set of output values for a functionSo this tells us it's not actually a function because for one x, number 1 there's actually two different y's So this is not a function if it's not a function it also cannot be 1 to 1 because part of being 1 to 1 is at first clause which means it also has to be a function So if you have no for function it can't be 1May 29, 18 · Relations Definition;



Prove The Existence Of A One To One Function For A Recursive Definition Mathematics Stack Exchange


Inverse Functions Examples Solutions Videos Activities
Composite functions and oneone onto;Definition Of One To One Function A function is said to be a OnetoOne Function, if for each element of range, there is a unique domain More About One to One Function Onetoone function satisfies both vertical line test as well as horizontal line testNov 12, 18 · In this section we will formally define relations and functions We also give a "working definition" of a function to help understand just what a function is We introduce function notation and work several examples illustrating how it works We also define the domain and range of a function In addition, we introduce piecewise functions in this section


One To One Functions Mathbitsnotebook Ccss Math


One To One Function Explanation Examples
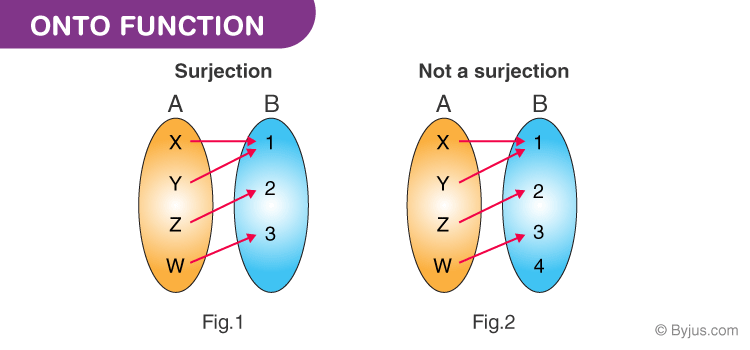
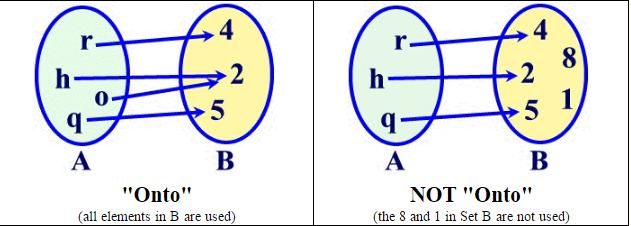
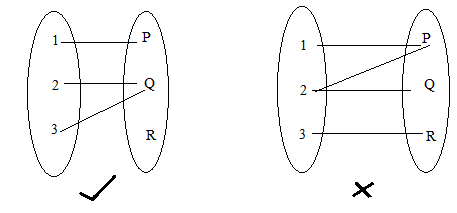
We call this relation as function f A → B ( f is a function from A to B ) Types of function Oneone Function or Injective Function If each elements of set A is connected with different elements of set BOnto Function Definition (Surjective Function) Onto function could be explained by considering two sets, Set A and Set B, which consist of elements If for every element of B, there is at least one or more than one element matching with A, then the function is said to be onto function or surjective function The term for the surjective functionDefine oneonone oneonone synonyms, oneonone pronunciation, oneonone translation, English dictionary definition of oneonone adj 1 Consisting of or being direct communication or exchange between two people oneonone instruction



One To One Functions Definitions And Examples Video Lesson Transcript Study Com



Relations And Functions Video Lessons Examples And Solutions
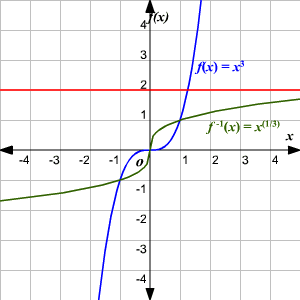
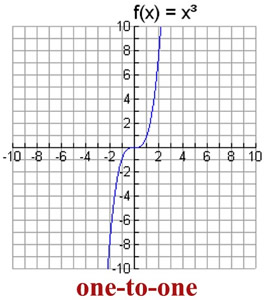
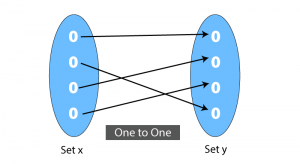
A function f from A to B is called onetoone (or 11) if whenever f (a) = f (b) then a = b No element of B is the image of more than one element in A In a onetoone function, given any y value, there is only one x that can be paired with the given y Such functions are also referred to as injectiveSeveral questions with detailed solutions as well as exercises with answers on one to one functions are presented One to One Function From the definition of onetoone functions we can write that a given function f (x) is onetoone if A is not equal to B then f (A) is not equal f (B)For each of the following functions, sketch a graph and then determine whether the function is onetoone 7 f x x 23 8 g x x2 5 9 h x x 2 3 10 f x x3 2 11 g x x 4 12 hx 3 1 x 13 f x x 21 2 14 g x x 6 Answer the following 15 If a function f is onetoone, then the inverse function, f 1, can be graphed by either of the following methods


Function Definition Types Examples Facts Britannica


One To One Functions
Function (mathematics) is defined as if each element of set A is connected with the elements of set B, it is not compulsory that all elements of set B are connected;Oct 24, · Let's start with this quick definition of one to one functions One to one functions are functions that return a unique range for each element in their domain Since one to one functions are special types of functions, it's best to review our knowledge of functions, their domain, and their rangeVirtual Nerd's patentpending tutorial system provides incontext information, hints, and links to supporting tutorials, synchronized with videos, each 3 to 7 minutes long In this nonlinear system, users are free to take whatever path through the material best serves their needs These unique features make Virtual Nerd a viable alternative to private tutoring



Finding The Inverse Of A Function Complete Guide Mashup Math



One To One Functions Ppt Video Online Download
Dec 09, · A function f from A to B is called onetoone (or 11) if whenever f (a) = f (b) then a = b No element of B is the image of more than one element in A In a onetoone function, given any y there is only one x that can be paired with the given yIn this video I want to introduce you to some terminology that will be useful in our discussion of functions and invertibility and this is in general terminology that you'll probably see in your mathematical careers so let's say I have a function f and it is a mapping from the set X to the set Y and we've drawn this diagram many times but it never hurts to draw it again so that is my set X orAllowing the pairing of each member of a class uniquely with a member of another class 2 Mathematics Relating to or being a correspondence between two sets that assigns to each member of one set exactly one member of the other set American Heritage® Dictionary of the English Language, Fifth Edition


One To One And Onto Functions Nool


Injections Surjections And Bijections Mathonline
F is onto, but it's from X to Y The onto function from Y to X is F's inverse Which must also be bijective, and therefore ontoOne To One Function One to one function is a function between 2 sets where every element in first set is mapped to only one element in second set based on that functionA onetoone function is a function where for each value y in the range of the function there is exactly one value x in the domain of the function A simple graphical method to check is a function



If Functions Are Aspirin Then How Do You Create The Headache Dy Dan



Mathwords One To One Function
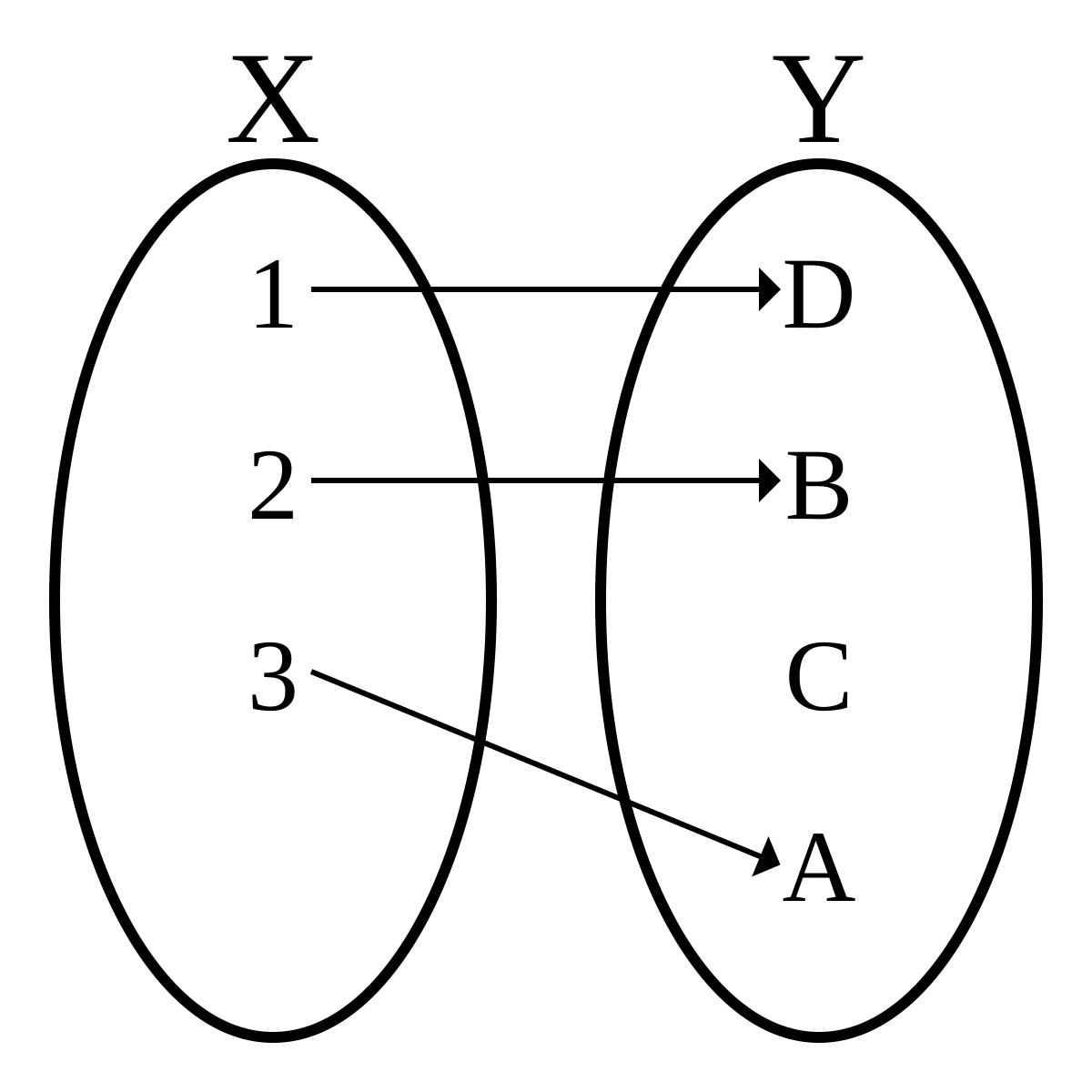
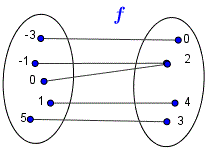
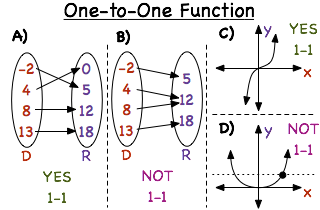
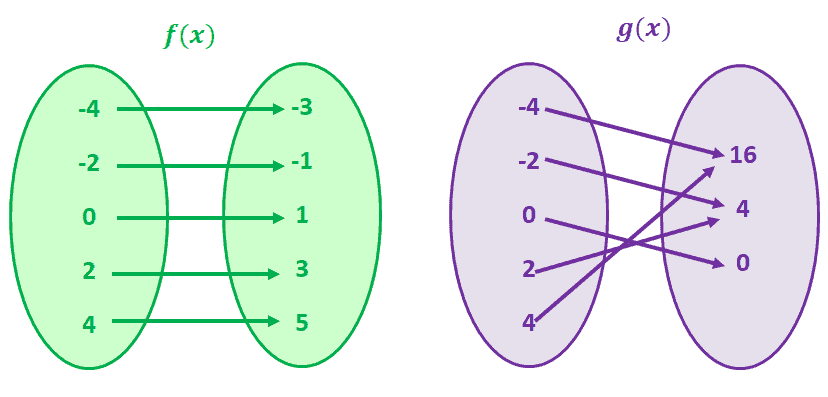
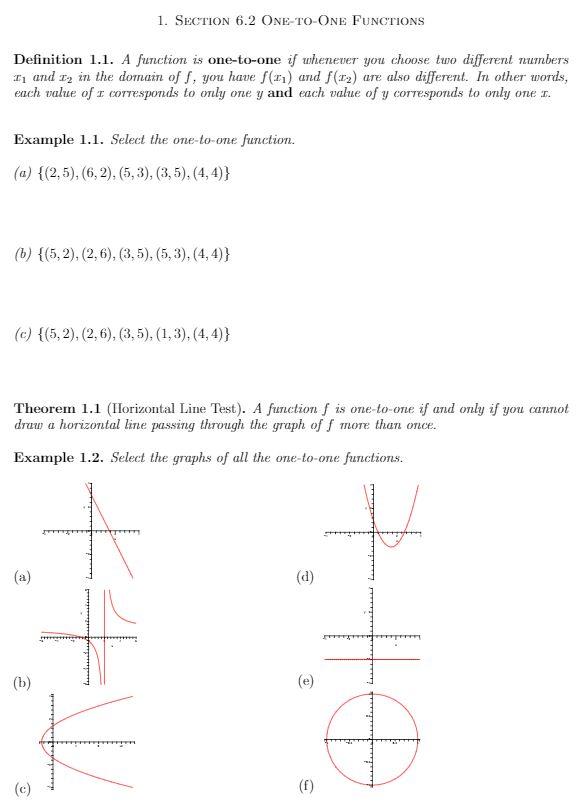
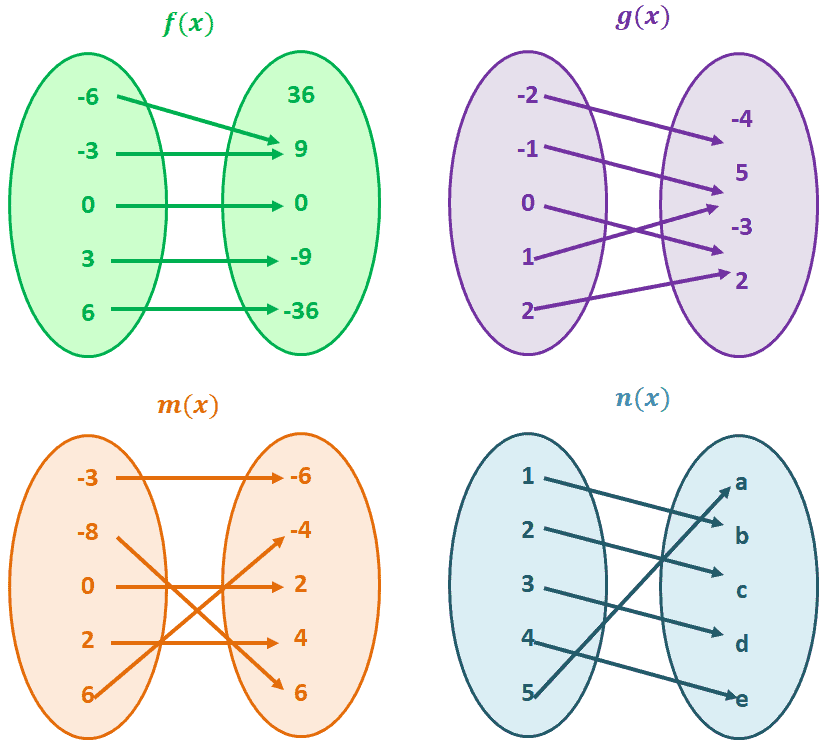
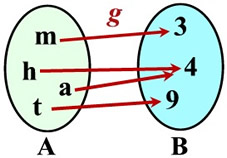
OnetoOne Function A mathematical function is defined as a relation in which every element in the range must be related to a different element in the domain It means no two outputs can be originated from the same input, ie for each x, there corresponds a single y pairing with xIn mathematics, an injective function (also known as injection, or onetoone function) is a function that maps distinct elements of its domain to distinct elements of its codomain In other words, every element of the function's codomain is the image of at most one element of its domain(a) Onetoone function, because each coordinate in the domain D has one and only one image in the range R (b) Not a function, because the coordinate 2 in the domain D has two images 3 and 5 in the range R (c) Not a onetoone function, because the coordinate 3 of range R is the image of both coordinates 2 and 6 of the domain D


One To One And Onto Functions Nool



Solved One To One And Onto Functions Definition 4 Let Chegg Com
Nov 12, 17 · Mathematics Stack Exchange is a question and answer site for people studying math at any level and professionals in related fields It only takes a minute to sign upFinding number of relations;Answer Yes a function should be strictly monotone to be defined as one to one function Reason If the function is not monotonous, then it can be a nonincreasing or



Abstract Algebra 1 Definition Of A Function Youtube



Function Definition And Many To One One To One Examples Youtube
Definition of one to one function and examplesتعريف الاقتران واحدلواحد مع أمثلةOne One Function Numerical Example 1Watch More Videos at https//wwwtutorialspointcom/videotutorials/indexhtmLecture By Er Ridhi Arora, Tutorials PointA function f (from set A to B) is bijective if, for every y in B, there is exactly one x in A such that f(x) = y Alternatively, f is bijective if it is a onetoone correspondence between those sets, in other words both injective and surjective



What Are One To One And Many To One Functions Quora



Definition Injection One To One Function Youtube
Apr 25, 18 · Any welldefined function is either onetoone or manytoone A function cannot be onetomany because no element can have multiple images The difference between onetoone and manytoone functions is whether there exist distinct elements that share the same image There are no repeated images in a onetoone function



Newgenedu


1


One To One Functions



Function Definitions


One To One Function Explanation Examples


One To One Functions
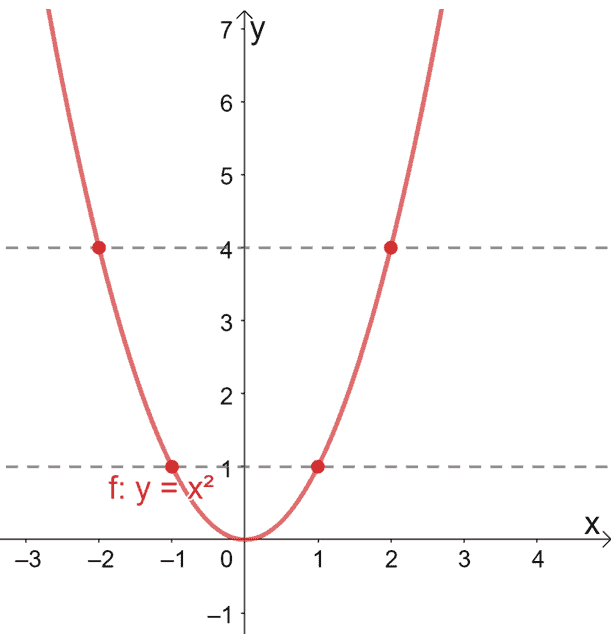


One To One Function Explanation Examples
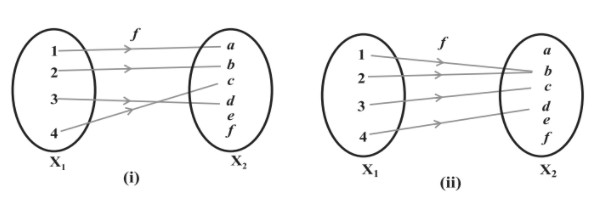


One To One Function Injective Function Definition Graph Examples


How To Prove That A Function Is Invertible If And Only If It Is Bijective Quora
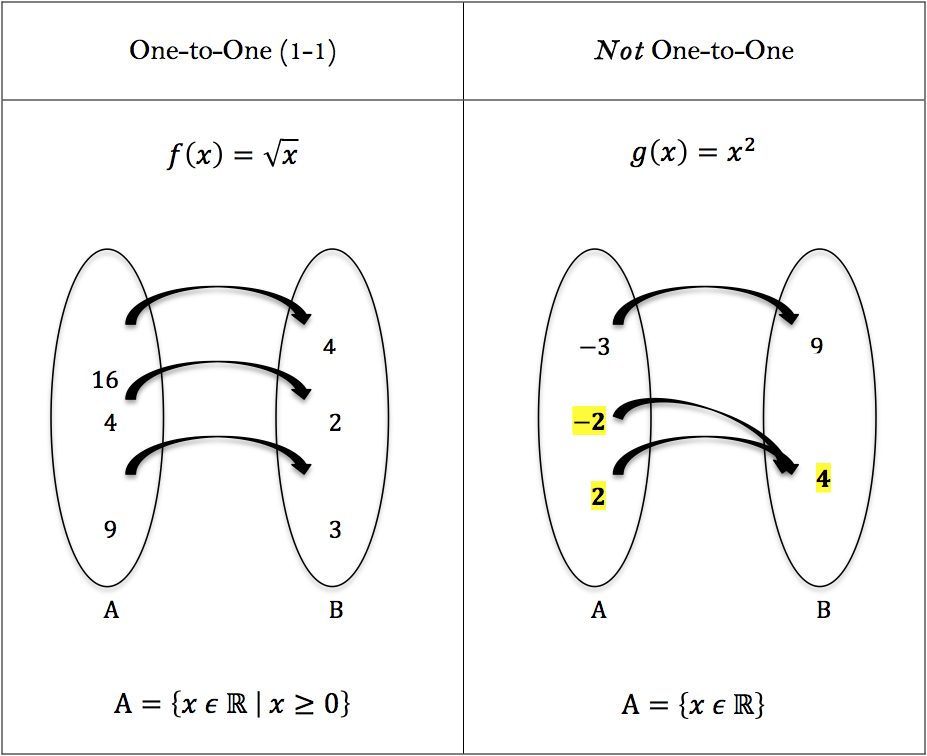


Functions And Their Inverses Worked Examples



One To One Function Definition Graph Examples A Level
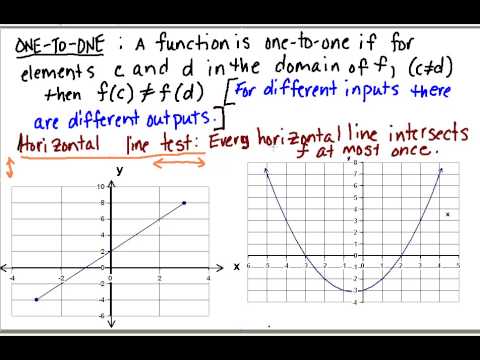


One To One Functions Youtube


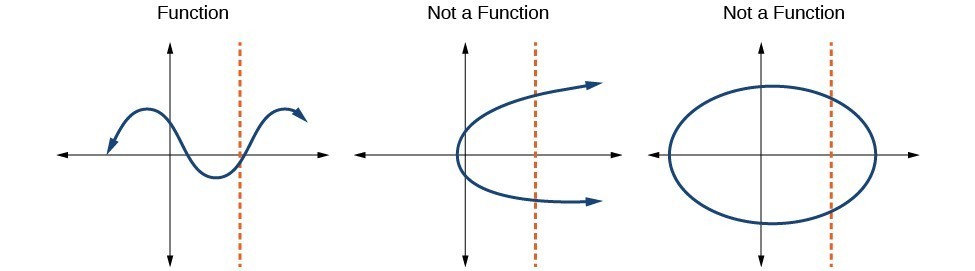
Identify Functions Using Graphs College Algebra



Inverse Function Wikipedia



Injective Surjective And Bijective


What Is A One To One Function Printable Summary Virtual Nerd



One To One Functions Definitions And Examples Video Lesson Transcript Study Com


One To One Function Is The Inverse Of A Function A 1 To 1 Function Is Just


Onto Function Definition Formula Properties Surjective Function



One To One Functions And Their Inverses Read Calculus Ck 12 Foundation


One To One Functions Section 3 7 Pp And Their Inverses Ppt Download


Identify Functions Using Graphs College Algebra



Cpsc125 Ch4 Sec4



Functions Sequences And Sums Ppt Video Online Download


One To One And Onto Functions A Plus Topper


One To One Function Injective Function Definition Graph Examples


One To One Functions Mathbitsnotebook Ccss Math


One To One Function Explanation Examples



One To One And Onto Functions A Plus Topper


Www Math Uh Edu Jiwenhe Math1432 Lectures Lecture01 Handout Pdf


Solved 1 Section 6 2 One To One Functions Definition 1 1 Chegg Com


One To One Function Explanation Examples



Injective Surjective And Bijective



2 7 One To One Functions And Their Inverses Flashcards Quizlet


One To One Functions Mathbitsnotebook Ccss Math


Relations And Functions Video Lessons Examples And Solutions


1


One To One Function Injective Function Definition Graph Examples



Definition Of An Injective Function Youtube


Functions Definition Types Domain Range And Video Lesson



One On One And Onto Function Mathematics Analysis
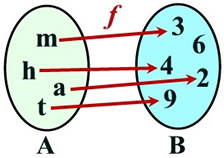


One To One Functions Mathbitsnotebook Ccss Math



Chapter 7 Functions In Laymans Terms A Function



What Is A Function Video Functions Khan Academy



If Functions Are Aspirin Then How Do You Create The Headache Dy Dan



One To One Functions Definitions And Examples Video Lesson Transcript Study Com



Function Definition And Many To One One To One Examples Youtube



Solved Use The Definition Of A One To One Function To Det Chegg Com
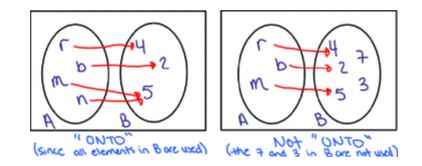


One To One And Onto Functions Nool


One One Onto Function Math World Only For Math Lovers



Functions And Limits Basic Definition And Formulas Mathematics Xii Mathematics Math Formulas Algebra Notes



Section 2 3 Section Summary Definition Of A Function O Domain Cdomain O Image Preimage One To One Injection Onto Surjection Bijection Ppt Download



5 1 Introduction To Functions



Definition Of One To One Functions Concept Algebra 2 Video By Brightstorm



Mapping Diagrams
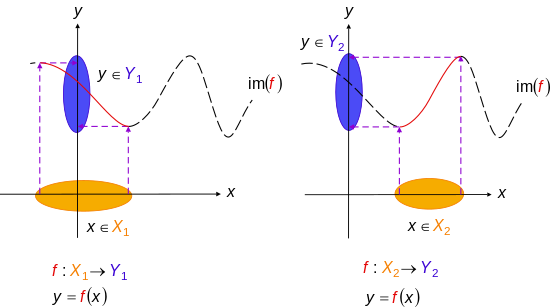


Injective Function Wikipedia


Definition Of The Term Function Zona Land Education



How To Determine Whether A Function Is One One Or Many One And Into Or Onto Quora



5 1 Introduction To Functions
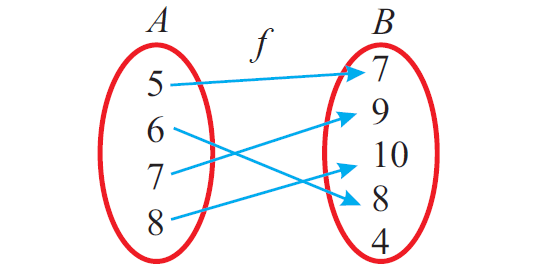


Unit 2 Relation And Function B C A Study


1
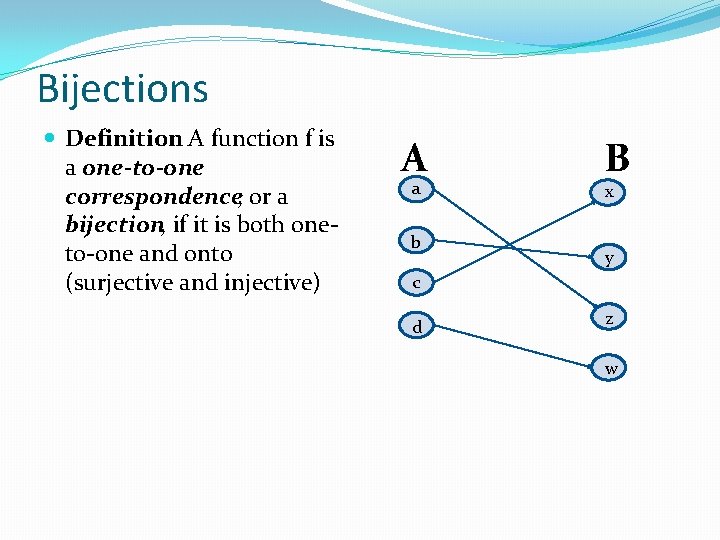


Functions Functions Definition A Function F From Set
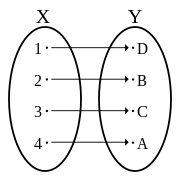


Injective Function Wikipedia



Section 2 8 One To One Functions And Their Inverses Ppt Download
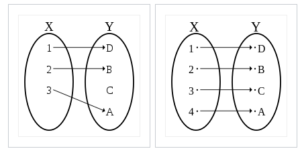


One To One Function Calculus How To
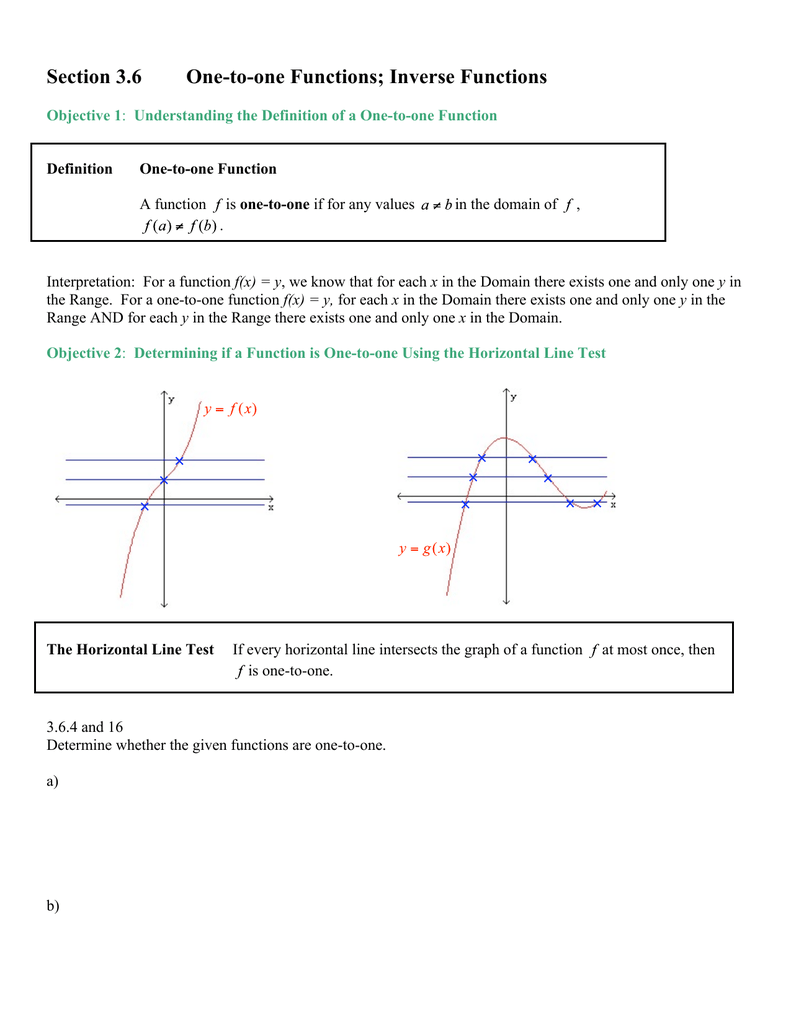


Section 3 6 One To One Functions Inverse Functions



Unit 2 Relation And Function B C A Study



Total Function Partial Function Definition Calculus How To



How To Prove A Function Is Injective One To One Using The Definition Math Videos Maths Exam Math



What Is One To One Function Definition And Meaning Math Dictionary


Different Types Of Functions Mathonline



Solved Note The Contrapositive Of The Definition Of One T Chegg Com



The Difference Between Inverse Function And A Function That Is Invertible Mathematics Stack Exchange



0 件のコメント:
コメントを投稿